Opdracht W3
Leg met de negen Pygramstukjes een figuur met een zo groot/klein mogelijke omtrek. Bereken de omtrek van je figuren door te stellen dat de zijden van het kleinste vierkantje lengte 1 hebben. De figuur hoeft niet convex te zijn , maar er mag geen gat in zitten. Stukjes mogen alleen tegen elkaar aan gelegd worden als hun zijden passen. Dat wil zeggen:of de tegen elkaar aan liggende zijden zijn even lang, of er passen meerdere stukjes precies tegen een grotere aan.
Voor de grootst mogelijke omtrek zorgden we ervoor dat elk stuk een verbinding met zijde 1 met een ander stuk heeft. Dan moet het wel een maximale omtrek geven.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
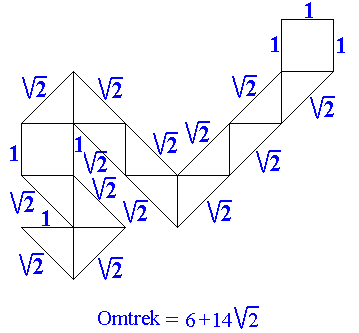
Onze maximale omtrek zonder het kleine vierkant is bij benadering 25,8.
Aangezien we geleerd hebben dat in het vlak de cirkel de figuur is die de kleinste omtrek heeft bij gelijke oppervlakte probeerden we dat met onze figuur te benaderen maar met de pygramstukjes valt dat niet echt mee.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
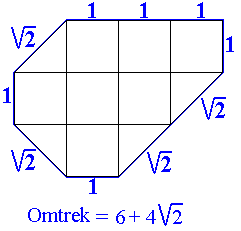
Onze kleinst mogelijke omtrek zonder het kleine vierkant is bij benadering 11,66
We hebben de voorkeur gegeven aan een convexe figuur.