Pygram

Dit is de Pythagorasprijsvraag 2007
De pygram bestaat uit negen stukken

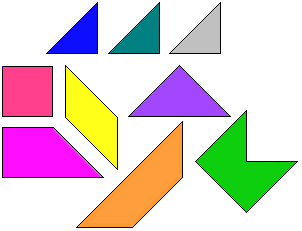
Hiermee kunnen we de "P" van de achtergrond maken.
We maakten een exel-file die heel handig is om vormen te zoeken. Eerst opslaan en dan openen in exel en zorgen dat werkbalk 'pentominos' geactiveerd is.

Laten we het vierkant weg dan blijven acht stukken over waarmee we de volgende rechthoek kunnen maken


Er zijn vier opdrachten in de categorie 'wiskundig' en twee in de categorie 'artistiek'

PYGRAM-WISKUNDIG
Opdracht W1
Gebruik de negen Pygramstukjes om zo veel mogelijk verschillende convexe figuren te maken. Twee figuren zijn verschillend als ze niet congruent zijn.
Een figuur heet convex als elke twee punten binnen de figuur verbonden kunnen worden door een lijnstuk dat zelf ook helemaal in die figuur ligt. (Er komen dus geen gaten of inhammen voor; de hoeken van de figuur zijn kleiner dan 180°)

Convexe figuren

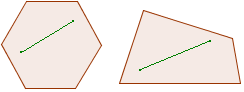Concave figuren

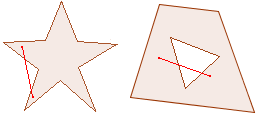Als we de negen stukjes beter bekijken zien we dat we in het totaal 18 congruente gelijkbenige rechthoekige driehoekjes hebben.
We zoeken alle convexe figuren die bestaan uit die 18 driehoekjes.

Opdracht W2
Laat het kleine vierkant weg. Gebruik de overige acht Pygramstukjes om zo veel mogelijk convexe figuren te maken. (je moet alle stukjes gebruiken).
Wat denk je, kun je met deze acht stukjes minder of juist meer convexe figuren maken dan met alle negen stukjes?

Opdracht W3
Leg met de negen Pygramstukjes een figuur met een zo groot/klein mogelijke omtrek. Bereken de omtrek van je figuren door te stellen dat de zijden van het kleinste vierkantje lengte 1 hebben. De figuur hoeft niet convex te zijn , maar er mag geen gat in zitten. Stukjes mogen alleen tegen elkaar aan gelegd worden als hun zijden passen. Dat wil zeggen:of de tegen elkaar aan liggende zijden zijn even lang, of er passen meerdere stukjes precies tegen een grotere aan.

Opdracht W4
Hetzelfde als W3, maar dan met weglating van het kleine vierkant.

PYGRAM-ARTISTIEK
Hier gelden geen beperkingen voor hoe je de stukjes neerlegt. Ze hoeven zelfs niet aan elkaar te liggen.

Opdracht A1
Kies een thema, bijvoorbeeld 'letters', 'verkeersborden' of 'vervoermiddelen'.
Maak met de Pygramstukjes zo veel mogelijk fraaie figuren die in het thema passen. Het is het mooist als je een thema volledig kunt invullen. Per figuur hoef je niet alle negen stukjes te gebruiken

Opdracht A2
Dit is een vrije opdracht, waar bijna alles mag: maak één of meer zo interessant mogelijke figuren. Je mag ook meerdere Pygramsetjes gebruiken, de stukjes (of de randen ) een kleur of een cijfer geven en dan voorwaarden bedenken waaraan je figuur moet voldoen, een bordspel met de Pygramstukken bedenken , ...