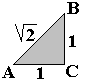
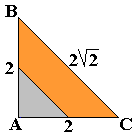
Pygram en
gelijkvormigheid
Dit zijn gelijkbenige rechthoekige driehoeken die je met de
pygramstukjes kan leggen.
Twee gelijkbenige rechthoekige driehoeken zijn altijd gelijkvormig. Weet je
waarom?
|
|
|
|
|
|
|
|
|
Het
potpourri probleem 36 op onze
pentominosite gaat over het verdelen van een figuur waarbij een
deel opnieuw een figuur is gelijkvormig met het geheel. We probeerden dit
met een pygramset.
Bekijken we de pygramstukjes:
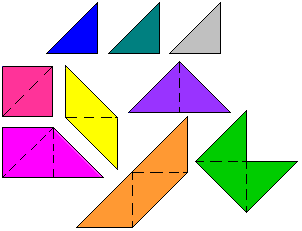
We hebben in totaal 18 driehoeken.
We kunnen 1 driehoek bekijken t.o.v. de gelijkbenige rechthoekige driehoek
die gevuld wordt met een pygramset (bestaat uit 18 driehoekjes).
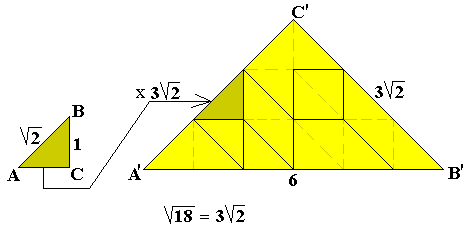
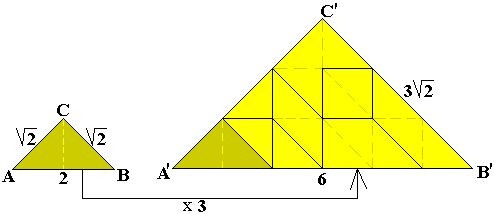
We kunnen een figuur gevormd door 2 driehoeken bekijken t.o.v. de
gelijkvormige figuur die gevuld wordt met een pygramset (bestaat uit 18
driehoekjes).
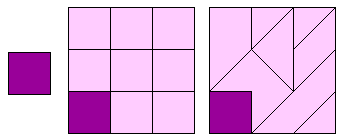
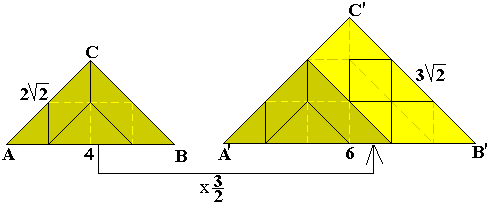
De gelijkvormigheidsfactor van het grote vierkant t.o.v. het pygramstukje is
3.
Merk op dat er 9 kleine vierkanten in de oppervlakte van het grote vierkant
zitten.
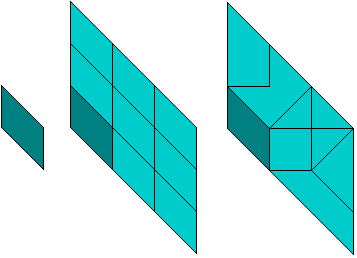
De gelijkvormigheidsfactor van de grote parallellogram t.o.v. het
pygramstukje is 3.
Merk op dat er 9 kleine parallellogrammen in de oppervlakte van de grote
zitten.
We kunnen een figuur gevormd door 3 driehoeken bekijken
t.o.v. de gelijkvormige figuur die gevuld wordt met een pygramset (bestaat
uit 18 driehoekjes).We kunnen zo'n figuur niet vinden omdat de oppervlakte
van de figuur is 18:3 is 6 maal groter, dus is de gelijkvormigheidsfactor de
vierkantswortel 6 en dat kunnen we niet leggen met pygramstukjes.
We kunnen een figuur gevormd door 4
driehoeken bekijken t.o.v. de gelijkvormige figuur die gevuld wordt met een
pygramset (bestaat uit 18 driehoekjes).
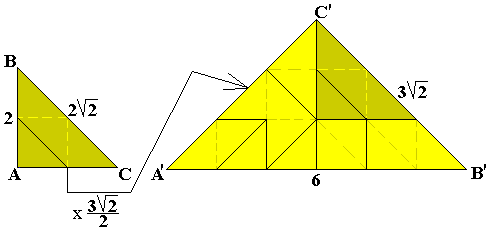
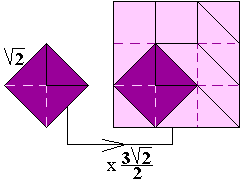
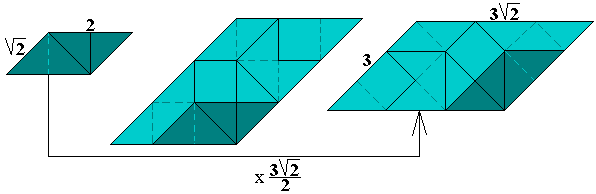
We kunnen een figuur gevormd door 8 driehoeken bekijken t.o.v. de
gelijkvormige figuur die gevuld wordt met een pygramset (bestaat uit 18
driehoekjes).
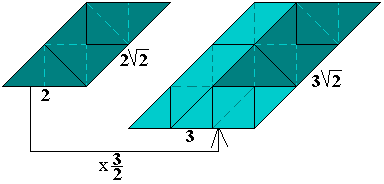
Opmerking: bij een vierkant kunnen we de rest van het groot vierkant niet
meer vullen met pygramstukjes.
We kunnen een figuur gevormd door 9
driehoeken bekijken t.o.v. de gelijkvormige figuur die gevuld wordt met een
pygramset (bestaat uit 18 driehoekjes).
Het
potpourri probleem 38 op onze
pentominosite gaat over het maken van een figuur met een gat
(oppervlakte S) dat gelijkvormig is met de figuur. Let ook even op de symmetrie.
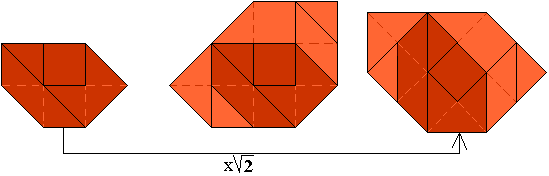
En nog een heel mooie:
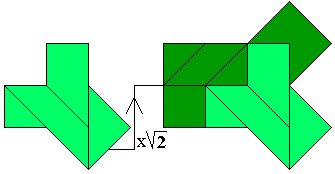
Je kan nog heel wat vormen vinden.
Heb je er een die we mogen op de site plaatsen mail dan naar
o.d.m@fulladsl.be
We kregen een mail van Helmut Postl uit Wenen
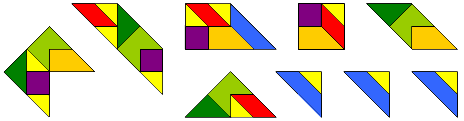
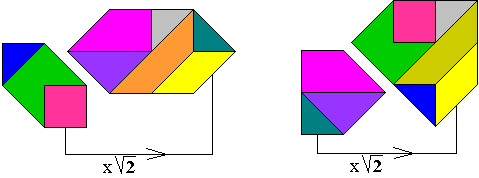
"Here are some more shapes where a pattern of 9 triangles is magnified by
the factor sqrt(2). The first three are turned over, the one at the right is
only rotated, and the last three have a horizontal symmetric axis. The
orange top triangle can be placed at the bottom right so to create the
mirror image of the shape."
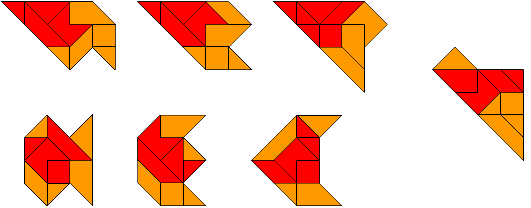
We bekeken ze nog eens afzonderlijk
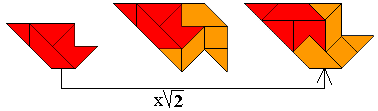
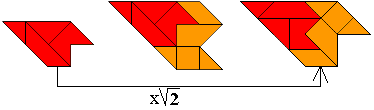
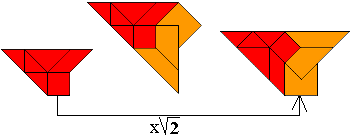
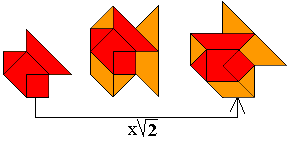
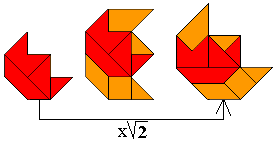
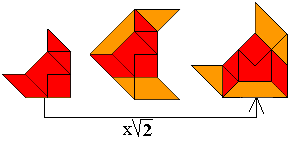
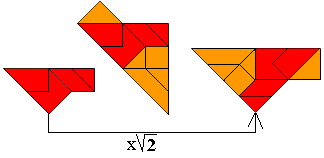
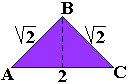
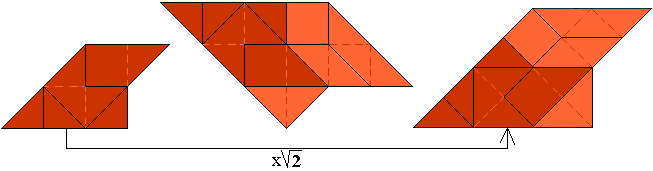
"Another magification: Take for example the first shape of the bottom
row. Turn it (2nd picture) and magnify it (3rd picture) so that the inner
pattern becomes the original outer pattern. (First row: a symmetric pattern.
Second row: a turned over pattern.) The orange area covers 9 triangles,
therefore the yellow area covers 18 triangles, and this corresponds to a
whole pygram set. So the task is to fill the yellow part with a pygram set."
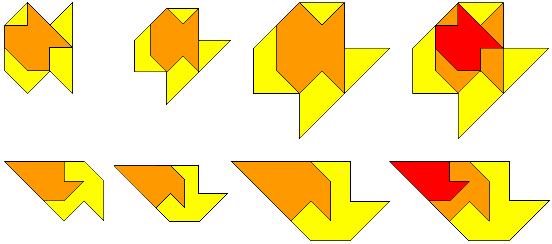
"Here are solutions, first the three patterns from your site, then my
patterns:"
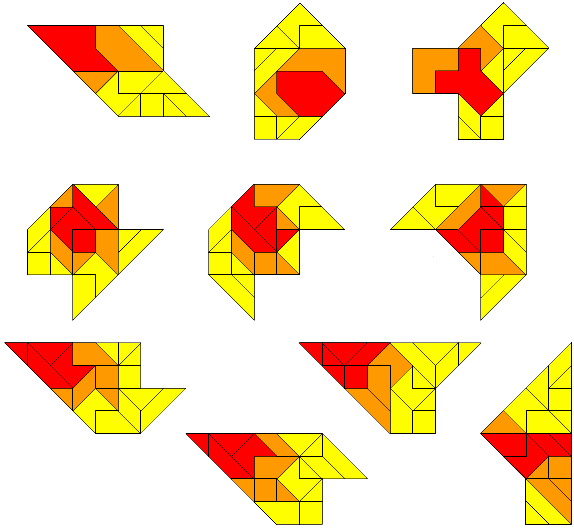
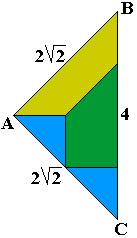
"Another idea: If we wanted to do another magnification, we get patterns
which are to be filled with two pygram sets. There I had the following idea:
If we can construct a magnified pygram set with two pygram sets, we can
immediately fill all magnified shapes. Unfortunately, this is not possible.
Proof: First, the two green pieces can only be placed as indicated (without
loss of generality). Next, the two blue pieces can only be placed as
indicated. Now we see that at the 1st, 3rd and 4th big piece we need at
least one big triangle and 3 small triangles. This leaves at most one big
triangle and 3 small triangles to be used for the other big pieces. But the
three triangles at the right side can only be filled with big and small
triangles, and we would need 3 big or 2 big + 2 small or 1 big + 4 small or
6 small triangles. In any case, we do not have enough triangles anymore.
Therefore the big pygram set cannot be built."

"A magnification by 4 however is possible:"
We probeerden dit
met een pygramset.
Als de gelijkvormigheidsfactor van de figuur t.o.v. het gat 2
is dan gaat de oppervlakte 4 maal groter zijn.
4S-S = 3S = 18 => S = 6
Op onze
pentominosite is er ook nog een
gelijkvormigheidsprobleem te vinden bij
congruentie.
Verdeel een pygramset in 3 groepen. Maak daarmee twee congruente figuren
(oppervlakte S) en een gelijkvormige figuur.
Het enige dat lukt is de gelijkvormigheidsfactor 2; de oppervlakte is dan
4S.
S+S+4S=18 => S=3
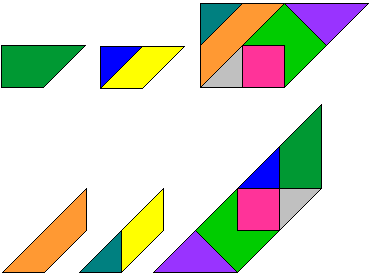
Met een pygramset is meer mogelijk dan met een pentominoset. (Onjuist
;-) We kunnen ook 2 gelijkvormige figuren maken met 1 set.
We kunnen de set verdelen in 2-16 (driehoeken).
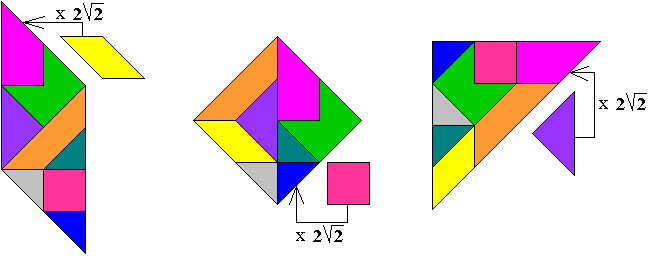
De verdeling waarbij we heel veel voorbeelden kunnen
vinden is 6-12.
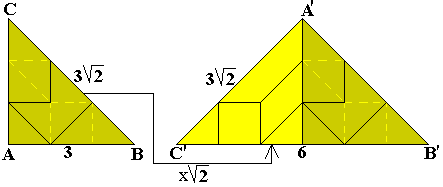
We begonnen met de vergroting van bestaande pygramstukjes (degene die uit 3
driehoeken bestaan)
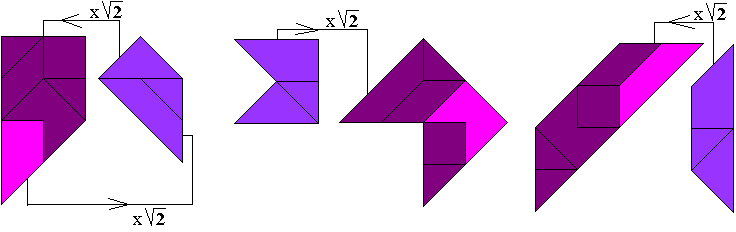
De vormen die we ook als gaten gevonden hebben:
En nog een paar omdat we ze leuk vinden.
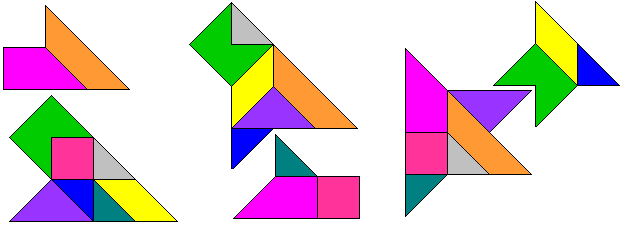
We krijgen er graag nog andere.
Ook opmerkingen zijn welkom.
o.d.m@fulladsl.be