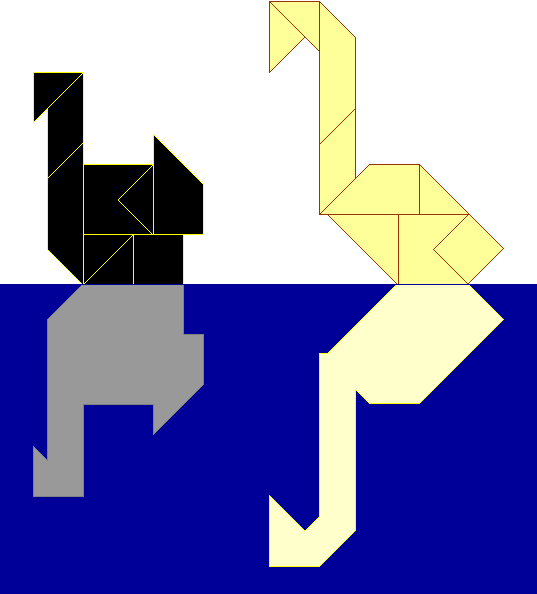PYGRAM-ARTISTIEK
Opdracht A2
Dit is een vrije opdracht, waar bijna alles mag: maak één of meer zo interessant mogelijke figuren. Je mag ook meerdere Pygramsetjes gebruiken, de stukjes (of de randen ) een kleur of een cijfer geven en dan voorwaarden bedenken waaraan je figuur moet voldoen, een bordspel met de Pygramstukken bedenken , ...

We breiden ons thema kerst verder uit naar deze opdracht met verschillende pygramsetjes.
De hulst werd gevuld met juist 5 setjes.


Met 7 setjes maakten we 9 kerstballen.
Ons thema symmetrie kan hier weer leuk aan bod komen: Welke kerstbollen hebben een symmetrie-as? We letten dus op de pygramstukjes en niet op het haakje van de bol.
Is er een bol tussen met een symmetriemiddelpunt?
Bij onze oplossing zijn er 5 ballen die een symmetrie-as hebben. Kan je nog beter?

Helmut Postl kon inderdaad nog veel beter. Hij heeft een set gemaakt met 8 achthoeken die een symmetrie-as hebben. Meer kan niet aangezien de rechthoekige trapezium geen symmetrie-as heeft en er juist 7 aanwezig zijn moet er dus een kerstbalversiering zijn met 1 (of 3)  trapezium die geen symmetrie-as heeft. Hetzelfde geldt voor de parallellogram.
Wil je Helmuts oplossing zien klik dan hieronder.
8 kerstballen die een symmetrie-as hebben.

trapezium We hebben een tweede stel in aanbieding, geschikt voor onze niet Nederlandstalige vrienden.
Is hier een kerstbal te vinden met een symmetrie-as?
En voor de allerkleinsten: vind de 2 gelijke kerstballen.


Onze kerstman gebruikte juist 8 pygramsets voor 9 pakjes te maken.
Welke pakjes hebben een symmetrie-as? We letten dus op de pygramstukjes en niet op de strik van het pakje
Is er een pakje bij met een symmetriemiddelpunt?
Bij onze oplossing zijn er 7 pakjes die een symmetrie-as hebben. Kan je nog beter?
Helmut Postl kon het in elk geval veel beter! Zijn 9 pakjes hebben allemaal een verticale symmetrie-as en zijn verschillend.
Voor zijn oplossing klik je op onze tekening.

Vind je twee dezelfde pakjes?

We maakten een spel van ons kerstpakje.

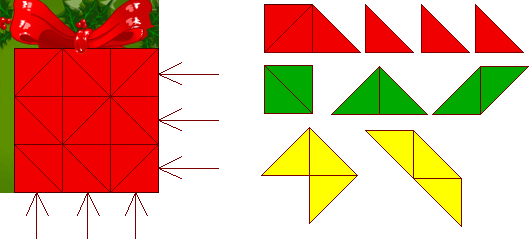
Plaats de cijfers van 1 tot 6 (in elk driehoekje één cijfer) op de pygramstukken zodat ze juist 1 keer voorkomen op dezelfde kleur.
 Plaats de pygramstukken in het vierkant (pakje) zodat op elke rij en op elke kolom de cijfers van 1 tot 6 juist éénmaal voorkomen .
De manier waarop de vierkanten in driehoeken verdeeld worden (in het pakje) is niet belangrijk.
De pygramstukken mogen gedraaid worden maar niet gespiegeld.
Het lijkt dus een beetje op een sudoku maar er is meer dan één oplossing.
Een oplossing kan je zien door te klikken op de opgave.

Omdat het niet elke dag kerstmis is maar sommige mensen elke dag een sudoku oplossen hebben we een Pygram-sudoku bedacht.

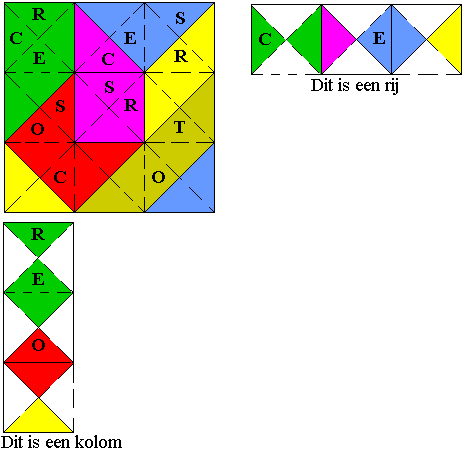Het bord is een vierkant gevuld met de pygramstukjes. Onze sudoku heeft 3 rijen en 3 kolommen. De Pygramstukjes hebben 6 verschillende kleuren. Op elke rij, in elke kolom en op elke kleur moet C,O,S,T,E en R juist éénmaal voorkomen.   Veel plezier! Er is juist 1 oplossing. Hiervoor zorgde Aad van de Wetering. Hij werkte ons idee uit. Heel veel dank. Wil je de oplossing? (Niet voor doorzetters) Druk dan op de opgave.

Hier is nog een andere (naar onze mening een makkelijker) opgave
Op elke rij, in elke kolom en op elke kleur moet 1,2,3,4,5 en 6 juist éénmaal voorkomen.

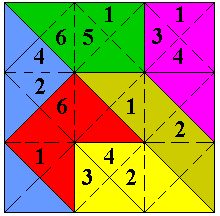
Voor de oplossing kan je op de opgave drukken.

Op de open school werd er druk gezocht om onze Pygram-sudoku op te lossen.

Wie wint het? Vader of zoon Lammens? De papa haalt het.

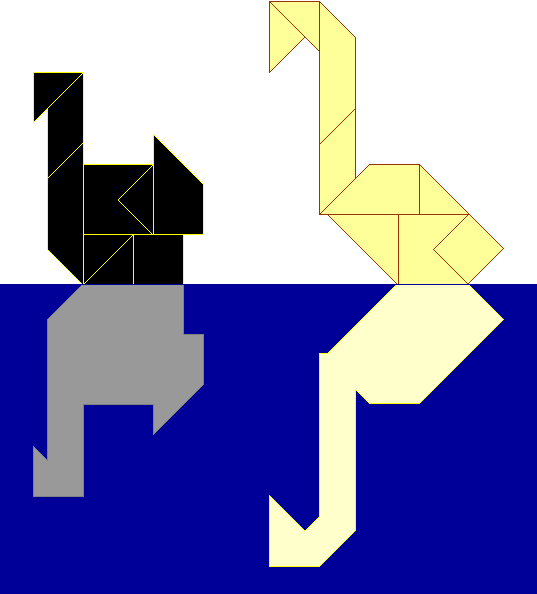
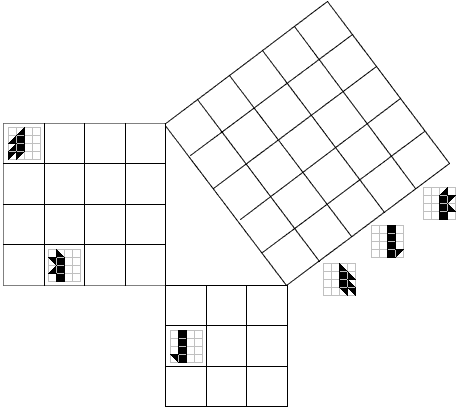
Mama Vanneste zoekt mee. En hier is het de papa die helpt Hanna maakte een eend en een zwaan. Gebruik 2 pygramsetten. Leg alle pygramstukken gespiegeld in het wateropppervlak en vul op die manier de spiegelbeelden op. En als afsluiter: speciaal voor Pythagoras maakten we een soort memoryspel op een voorstelling van de stelling. We maakten dus 2 sets van 25 kaartjes. De eerste set kaartjes worden in de vierkanten van 3x3 en 4x4 gelegd. De tweede set bestaat uit de spiegelbeelden en worden in het vierkant van 5x5 gelegd. We zien hier nog maar eens dat 3²+4²=5². 2B2 tekende eerst de spiegelbeelden van de gekregen opgaven. Nadien werden ze gekleurd om het memospel een beetje makkelijker te maken.   Jeremy had thuis zijn kaartjes mooi ingekleurd! Deel van onze tafel op de open school Wil je ook onze kaartjes maken? Je vind hieronder de opgaven.   Verticale symmetrie-as Reeks 1 Reeks 2 Reeks 3 Reeks 4 Reeks 5 Schuine symmetrie-as Reeks 1 Reeks 2 Reeks 3 Reeks 4 Men kan beginnen spelen met de kaartjes naar de speler toe. Iets moeilijker wordt het als men de kaartjes draait. Men kan ook pas een punt toekennen als men de figuur gemaakt heeft met een pygramset. Ter gelegenheid van kerst maakte Maxime Geenens voor ons mooie versierde bierkaartjes waarop we de tekeningen aanbrachten. Deze bierkaartjes zijn ook heel mooi als we er een vorm op tekenen die men dan moet met de pygramstukken proberen te maken. Gezellig tussen pot en pint met Pygram ;-) 2B1 tekende de vormen door telkens het spiegelbeeld te tekenen. Onze vormen op de kaartjes hebben een schuine symmetrie-as. Kimberly vond in de klas reeds een aantal vormen met de pygramstukjes en Salima maakte thuis een hele set.