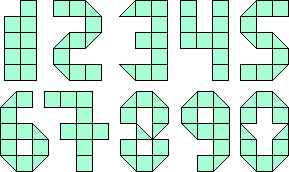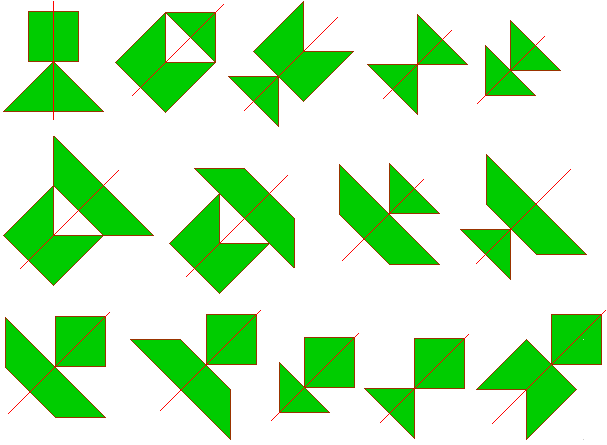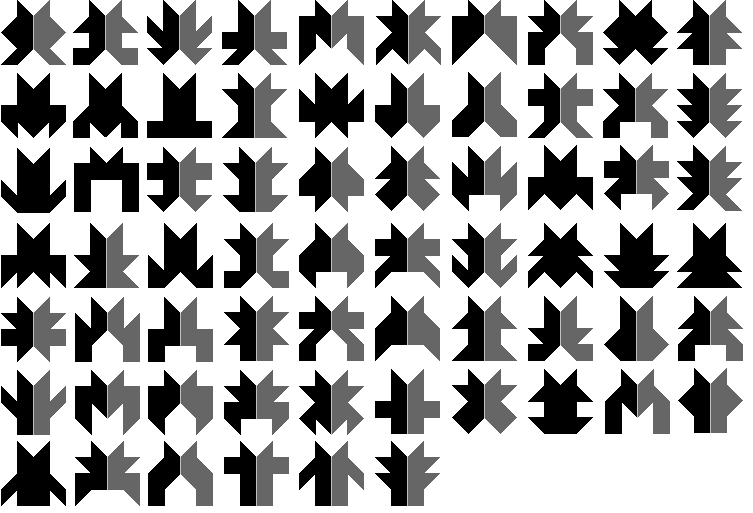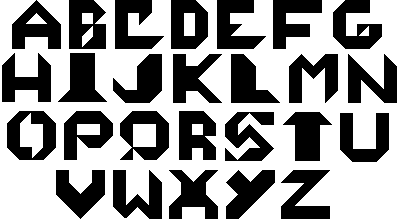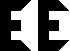PYGRAM-ARTISTIEK
Opdracht A1
Hier gelden geen beperkingen
voor hoe je de stukjes neerlegt. Ze hoeven zelfs niet aan elkaar te liggen.
Kies een thema, bijvoorbeeld
'letters', 'verkeersborden' of 'vervoermiddelen'.
Maak met de Pygramstukjes zo veel mogelijk fraaie figuren die in het thema
passen. Het is het mooist als je een thema volledig kunt invullen. Per
figuur hoef je niet alle negen stukjes te gebruiken
We kregen van Aad van de Wetering alle
cijfers.
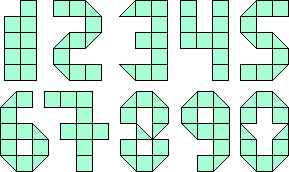
Ga met de muisaanwijzer over de vorm
en je ziet een oplossing.
De "1" vonden we niet goed geslaagd. Aad stuurde een betere maar dan niet
met de volledige pygramset.
We maakten er zelf ook een.De onze is ook 5 hoog.
Voor het nieuwe jaar pasten we Aads
raadsel een beetje aan.

Oplossing
Als thema kozen we
SYMMETRIE.
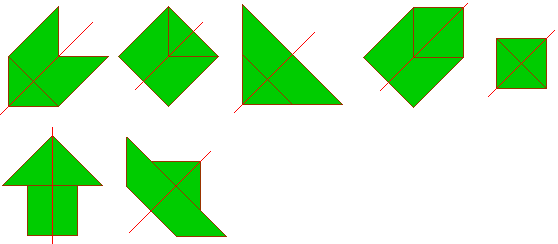
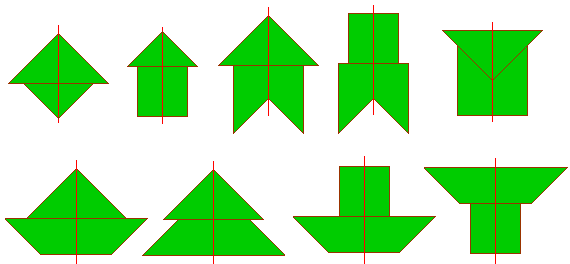
We zochten naar symmetrie-assen bij elk pygramstukje.

We zochten alle vormen die we met 2 Pygramstukjes konden maken die een
symmetrie-as hebben, als we ook op de verdeling van de pygramstukjes letten.
|
De Pygramstukjes liggen op het raster
Bij de laatste 2 passen de zijden niet |
|
Sommige Pygramstukjes liggen niet
op het raster: ze zijn 45° gedraaid.
Met een beetje fantasie zien we de kop van een Chinees mannetje, een
hut, raketten, altaar, boten, kandelaars, kandelaar met kaars en een
dennenboom. |
|
De Pygramstukjes liggen op het raster, maar er zijn puntcontacten.
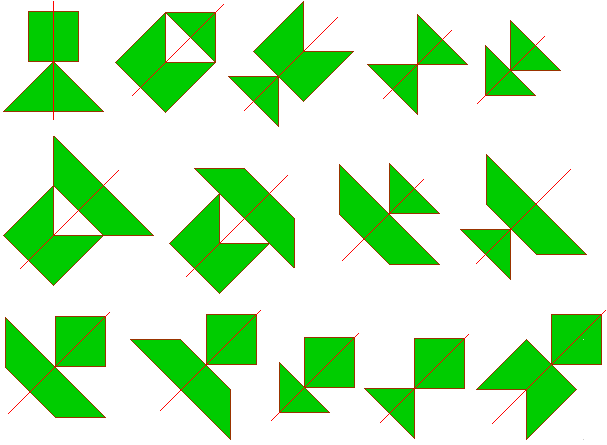
|
|
Sommige Pygramstukjes liggen niet
op het raster: ze zijn 45° gedraaid,
maar er zijn puntcontacten.
 |
Uitdaging:
Zoek alle vormen met 3 Pygramstukjes die een symmetrie-as hebben, als je ook
op de verdeling van de pygramstukjes let.
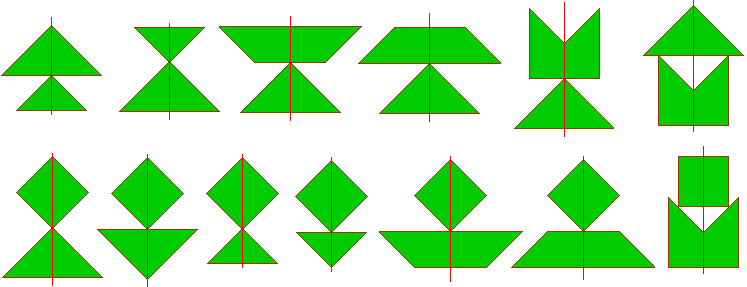
Als volgende opdracht zochten we alle figuren gevuld met een
pygramset die een symmetrie-as of een symmetriemiddelpunt bezitten. Alvast
kwamen we tot de constatie dat dit wel een heel grote opdracht was vooral
als de jury het thema mooist vindt als het volledig is. We gingen dus ons
thema wat beter omschrijven om het te beperken. We zochten alle figuren
binnen een vierkant van 4x4 die een verticale symmetrie-as hebben. We
beperkten ons tot figuren zonder gaten en waarbij de stukjes met elkaar een
zijde gemeenschappelijk hebben.
We hebben
er 347 gevonden.
Hieronder zie je alle vormen. Sommige vormen worden door de symmetrie-as
verdeeld in twee vormen die elk te vullen zijn met pygramstukken: zijn de
zwart-donkergrijze figuren.
Ga met de muisaanwijzer over de vorm
en je ziet een oplossing.

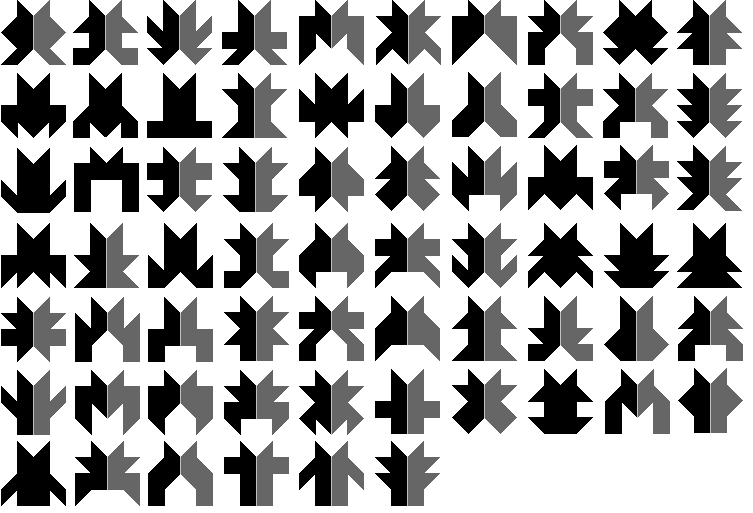
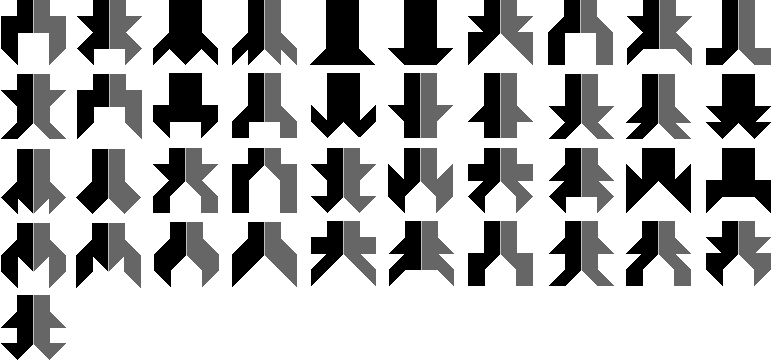
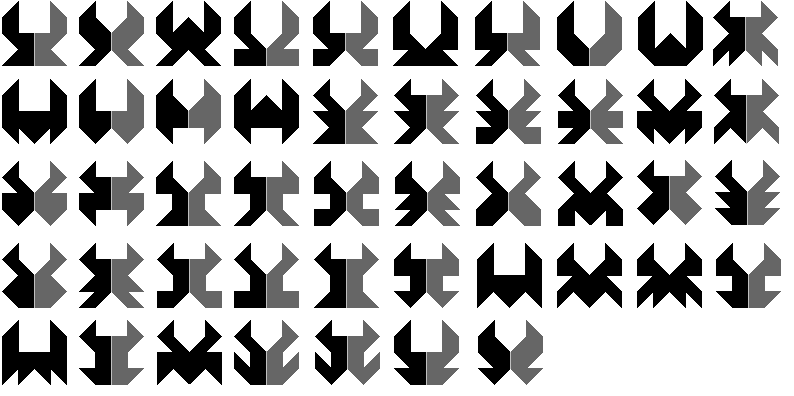
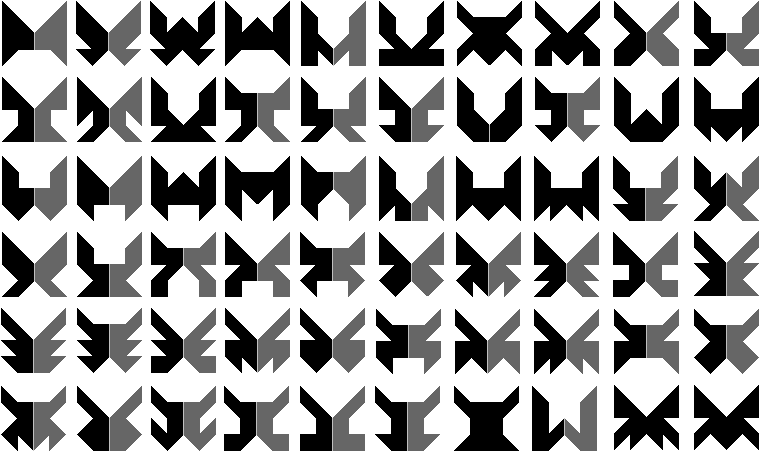
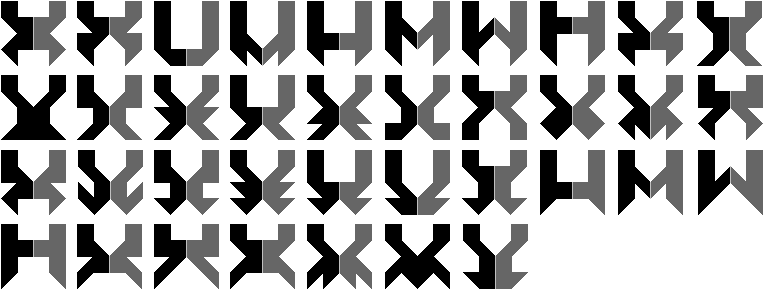
We dachten eraan alle vormen
binnen een vierkant van 4x4 te zoeken
die een schuine symmetrie-as hebben.Na heel wat zoekwerk gingen we te rade
bij Helmut Postl. Hij vond er 543.
Wil je ze graag zien? Stuur een mail naar
o.d.m@fulladsl.be
Ook zijn mening klopte met de onze: "I think, there
are too many to list all of them.
Here I will
show some general constructions how to build symmetric patterns."
Dit was zo mooi uitgelegd dat we een pagina maakten die je vindt door te
klikken op "Here"
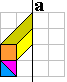
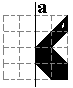
Teken de volgende figuren. Je vindt ze door het spiegelbeeld in a van de
linkerhelft te tekenen. Vul nadien op met de resterende pygramstukken.
Toegangspoort 1
 |
Toegangspoort 2
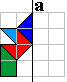 |
Toegangspoort 3
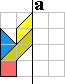 |
Toegangspoort 4
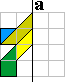 |
Raket
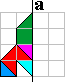 |
Dennenboom
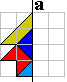 |
Suikertang
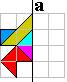 |
Vogelvoedselkastje
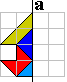 |
Kever
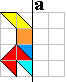 |
Speerpunt
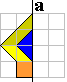 |
Kleedje
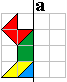 |
Stierekop
 |
Badia op zoek naar de spiegelbeelden.

Wil je meer foto's zien van 2B tijdens de wiskundeles klik dan op
bovenstaande foto.
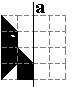
Maak de volgende figuren af. Je vindt ze door het spiegelbeeld in a te
tekenen. Vul nadien de volledige vorm op met een pygramset.
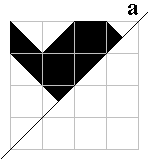
Bolhoed |
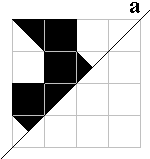
Arend |
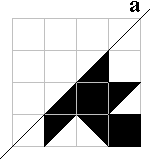
Vleermuis |
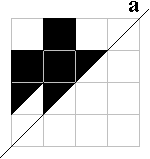
Krab |
|
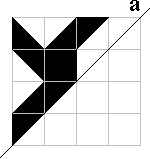
Fopspeen |
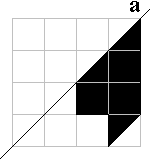
Deltavlieger |
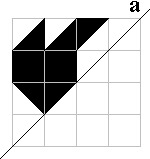
Stekker |
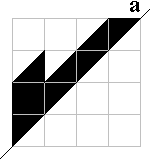
Xafax sleutel |
Bij de vleermuis, de krab, het fopspeen,de deltavlieger en
de stekker zijn beide helften met een aantal pygramstukken te vullen.
Bij de bolhoed en de arend lukt dat niet. Zie je waarom het zeker niet kan?
Dank zij het programma dat
Aad van de Wetering voor ons maakte weten
we zeker dat dit bij de Xafax sleutel ook niet lukt.
Bij onze deltavlieger ligt er een link naar het mooie gedicht "Vlieger" van
Drs. P en Marjolein Kool.
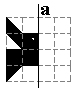
In een vierkant van 4x4 vonden we 4 vormen met 2 schuine symmetrie-assen.
Hieronder kan je er 3 ontdekken door het gegeven stuk te spiegelen in a, te
spiegelen in b en te puntspiegelen in O.
Leg daarna de vorm met de pygramstukken.
Vind je de
vierde vorm?
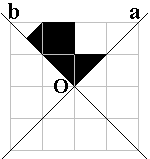
Accordeon |
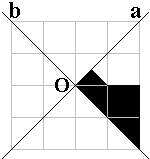
Bot |
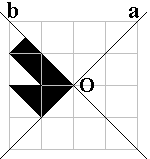
Orthodox Kruis |
Hier vind je 4 bladen met 6 kaartjes.
Reeks 1
- Reeks 2 -
Reeks 3
- Reeks
4
De figuren op de kaartjes moeten gespiegels worden in een schuine symmetrie-as. Vul nadien de volledige vorm op met een pygramset.
Hier zie je enkele van onze eendjes met hun spiegelbeeld in het water. Vul
de eendjes en hun spiegelbeeld met een pygramset.

Wil je het eerst iets makkelijker? Vul de spiegelbeelden met de resterende
pygramstukken.

Teken de volgende verkeersborden volledig door het spiegelbeeld in a te
tekenen van het gegeven gedeelte.
Vul nadien telkens de pijl met een pygramset. Vind je het lastig? Ga dan met
de muisaanwijzer over het verkeersbord.
Onze symmetrische kaarsen horen leuk bij de uitwerking van ons thema
symmetrie rond kerst maar kaarsen worden het ganse jaar gebruikt.
Bij de eerste twee moet je de kaars vullen met de rest van de pygramstukjes.
Bij de laatste opgave moet je de kandelaar maken met de 7 overblijvende
pygramstukjes.
De oplossing is te zien als je de kaars aanwijst.
We kunnen ook 2 dezelfde figuren zien in één vorm als we
naar het spiegelbeeld kijken.
Frank Potts
had hetzelfde idee.

The front of this card shows a Santa hiding behind a candlestick, or does
it? Is it 2 Santa’s facing each other?
Jan Kok ziet een bewijs van de wiskundige paradox 1=2 en iemand anders ziet
zelfs twee kandelaars en acht kerstmannen. Deze laatste weet niet waarom maar
ja 't is oudejaar geweest ;-)
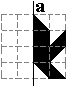
Ven de volgende figuren zijn er telkens 2. Teken zelf de tweede door het spiegelbeeld in a te
tekenen. Vul ze nadien met een pygramset. Ze zijn ook telkens afzonderlijk
met een aantal stukken te vullen. De oplossing is hierboven tussen de 347
vormen te vinden.
|
Reikhalzende ganzen |

Kabouters rug aan rug |
Zittende mannekes |
Engelen |
|

Kussende heksen |
Kolibries |

Koninginnen |
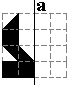
Boekenhouders |
|
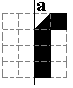
Wandelstokken |
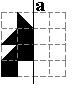
Vrouwen met boerka
in gesprek |
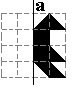
Chineze vrouwkes
rug aan rug |
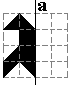
Chineze vrouwkes
aan het rusten |
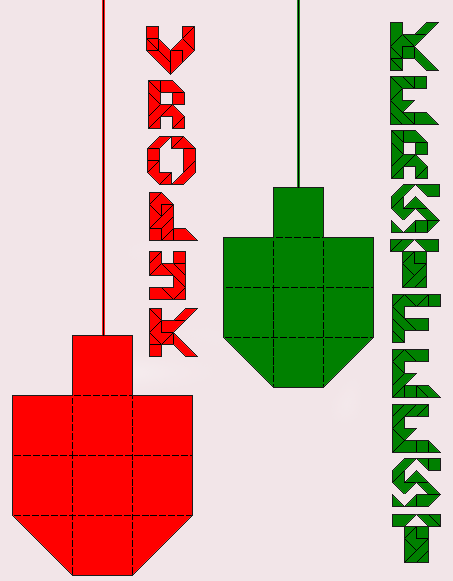
Ter gelegenheid van de kerst- en nieuwjaarsdagen maakten we een aantal leuke
kaartjes waarbij symmetrie troef is.
Ga met de muisaanwijzer over de vorm
en je ziet een oplossing.
Onze tekening zit vol met pygramfiguren die een symmetrieas bezitten. Kan je
ze allemaal vinden?
De letters V,K en T, de kerststal, Maria, Jozef, de kribbe, de dennenboom,
de kerstballen.
De ster heeft 4 symmetrie-assen maar is de enige figuur die niet met een
volledige set gemaakt is.
De letter O heeft een symmetrie-middelpunt alsook de ster.

Een ander ontwerp met een symmetrische
kerstboom binnen een vierkant van 4x4:

Bij dit kerstkaartje worden de
pygramstukjes wel erg klein.
De kerstboompjes zijn mooie voorbeelden van gelijkvormige figuren.
We verkozen zelf het volgende ontwerp:
Onze beste vrienden stuurden we de
klasfoto. Zelfs de weergoden waren ons gunstig gezind zodat elke plaats in
de hof schitterend was voor de foto.
Aangezien Helmut Postl ons heel veel hielp
met het zoeken van alle symmetrische oplossingen maakten we voor hem iets
speciaal.

Bij het maken van onze wensen hadden we
nogal wat letters nodig. Daarom maakten we het alfabet.
Deze letters zijn allemaal 4 hoog en met een volledige set gemaakt. Hierdoor
moeten sommige letters wel inleveren aan schoonheid.
Een aantal letters hebben een symmetrie-as. Kan je die vinden?
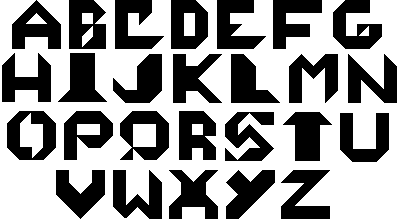
Enkele letters maakten we mooier.
We maakten de "E" 5 hoog. Nu heeft ze bovendien een symmetrie-as.
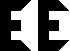
Deze letters zijn hoogte 4 en te vullen met een pygramset.
Behalve N en IJ heeft de rest een symmetrie-as.

Van Aad van de Wetering kergen we de volgende initialen. Dank je wel. Ze
zijn gemaakt met 3 pygramsets maar niet per letter.
We maakten er zelf een waarbij elke letter bestaat uit een set en ook een
symmetrie-as heeft.
Ga met de muisaanwijzer over de vorm
en je ziet een oplossing.
En van wie zijn deze initialen?

We maakten een leuk kerstpakje voor onder de kerstboom. Aad van de Wetering
mag er eentje verwachten als dank voor het maken van een Pygram-programma.

En als afsluiter: speciaal voor
Pythagoras.
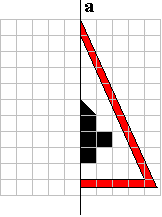
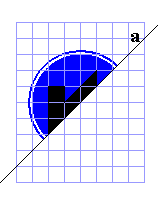
Deze voorstelling van de stelling van Pythagoras bevat juist 18 driehoeken
en kan dus gemaakt worden met een pygramset!
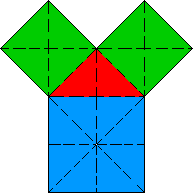
De figuur kan bovendien gelegd worden in een vierkant van 4x4 en heeft een
verticale symmetrie-as. We kunnen elke helft vullen met een aantal
pygramstukken.
Voor wie het eenvoudiger wil: