PYGRAM-WISKUNDIG
Opdracht W1
Gebruik de negen Pygramstukjes om zo veel mogelijk verschillende convexe figuren te maken. Twee figuren zijn verschillend als ze niet congruent zijn.
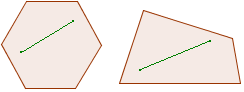
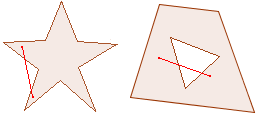
Een figuur heet convex als elke twee punten binnen de figuur verbonden kunnen worden door een lijnstuk dat zelf ook helemaal in die figuur ligt. (Er komen dus geen gaten of inhammen voor; de hoeken van de figuur zijn kleiner dan 180°)

Convexe figuren

Concave figuren

Als we de negen stukjes beter bekijken zien we dat we in het totaal 18 congruente gelijkbenige rechthoekige driehoekjes hebben.
We zoeken alle convexe figuren die bestaan uit die 18 driehoekjes.

We zoeken naar convexe figuren naargelang de omgeschreven rechthoek.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing

2x5 rechthoek

2x6 rechthoek

3x3 rechthoek

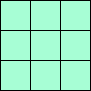3x4 rechthoek

 

4x4 rechthoek

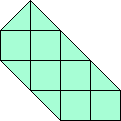6x3 rechthoek

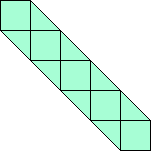
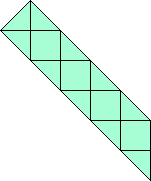
Deze stropdas en mes kregen we van Aad van de Wetering. 5x5 rechthoek 5x6 rechthoek